Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 178, pp. 1-13.
Kirchhoff type problems with potential well and indefinite potential
Yuanze Wu, Yisheng Huang, Zeng Liu
Abstract:
In this article, we study the Kirchhoff type problem
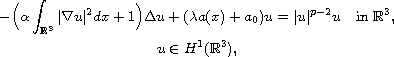
where
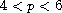 ,
,
 and
and
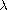 are two positive parameters,
are two positive parameters,
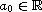 is a (possibly negative) constant and
is a (possibly negative) constant and
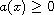 is
the potential well. Using the variational method, we show the existence
of nontrivial solutions. We also obtain the concentration behavior
of the solutions as
is
the potential well. Using the variational method, we show the existence
of nontrivial solutions. We also obtain the concentration behavior
of the solutions as
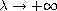 .
.
Submitted February 19, 2016. Published July 6, 2016.
Math Subject Classifications: 35B38, 35B40, 35J10, 35J20.
Key Words: Kirchhoff type problem; indefinite potential; potential well;
variational method.
Show me the PDF file (283 KB),
TEX file for this article.
 |
Yuanze Wu
College of Sciences
China University of Mining and Technology
Xuzhou 221116, China
email: wuyz850306@cumt.edu.cn
|
|---|
 |
Yisheng Huang
Department of Mathematics
Soochow University, Suzhou 215006, China
email: yishengh@suda.edu.cn
|
|---|
 |
Zeng Liu
Department of Mathematics
Suzhou University of Science and Technology
Suzhou 215009, China
email: luckliuz@163.com
|
|---|
Return to the EJDE web page
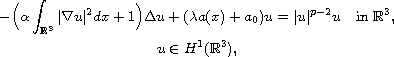
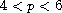 ,
,
 and
and
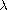 are two positive parameters,
are two positive parameters,
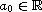 is a (possibly negative) constant and
is a (possibly negative) constant and
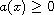 is
the potential well. Using the variational method, we show the existence
of nontrivial solutions. We also obtain the concentration behavior
of the solutions as
is
the potential well. Using the variational method, we show the existence
of nontrivial solutions. We also obtain the concentration behavior
of the solutions as
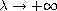 .
.


