Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 176, pp. 1-21.
Boundedness in a three-dimensional attraction-repulsion
chemotaxis system with nonlinear diffusion and logistic source
Yilong Wang
Abstract:
This article concerns the attraction-repulsion chemotaxis system with
nonlinear diffusion and logistic source,
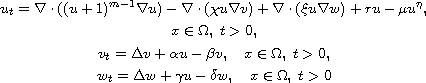
under Neumann boundary conditions in a bounded domain
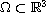 with smooth boundary.
We show that if the diffusion is strong enough or
the logistic dampening is sufficiently powerful, then the corresponding
system possesses a global bounded classical solution for any sufficiently
regular initial data. Moreover, it is proved that if
with smooth boundary.
We show that if the diffusion is strong enough or
the logistic dampening is sufficiently powerful, then the corresponding
system possesses a global bounded classical solution for any sufficiently
regular initial data. Moreover, it is proved that if
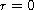 ,
,
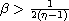 and
and
 for the latter case,
then
for the latter case,
then
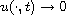 ,
,
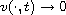 and
and
 in
in
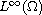 as
as
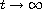 .
.
Submitted February 8, 2016. Published July 6, 2016.
Math Subject Classifications: 35K55, 35Q35, 35Q92, 92C17.
Key Words: Chemotaxis; attraction-repulsion; boundedness; nonlinear diffusion;
logistic source.
Show me the PDF file (316 KB),
TEX file for this article.
 |
Yilong Wang
School of Sciences
Southwest Petroleum University
Chengdu 610500, China
email: wangelongelone@163.com
|
|---|
Return to the EJDE web page
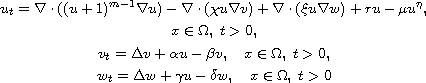
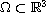 with smooth boundary.
We show that if the diffusion is strong enough or
the logistic dampening is sufficiently powerful, then the corresponding
system possesses a global bounded classical solution for any sufficiently
regular initial data. Moreover, it is proved that if
with smooth boundary.
We show that if the diffusion is strong enough or
the logistic dampening is sufficiently powerful, then the corresponding
system possesses a global bounded classical solution for any sufficiently
regular initial data. Moreover, it is proved that if
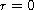 ,
,
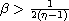 and
and
 for the latter case,
then
for the latter case,
then
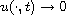 ,
,
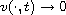 and
and
 in
in
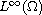 as
as
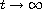 .
.
