In this article, we study the existence and infinitely many solutions for the elliptic boundary-value problem
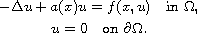
Our main tools are the local linking and symmetric mountain pass theorem in critical point theory.
Hui-Lan Pan, Chun-Lei Tang
Abstract:
In this article, we study the existence and infinitely many
solutions for the elliptic boundary-value problem
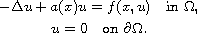
Our main tools are the local linking and symmetric mountain pass theorem in
critical point theory.
Submitted April 7, 2016. Published June 29, 2016.
Math Subject Classifications: 35J61, 35D30, 35J20.
Key Words: Super-quadratic condition; variational method; Cerami condition;
critical point theory.
Show me the PDF file (233 KB), TEX file for this article.
 |
Hui-Lan Pan School of Mathematics and Statistics Southwest University Chongqing 400715, China email: panhuilanswedu@163.com |
|---|---|
 |
Chun-Lei Tang School of Mathematics and Statistics Southwest University Chongqing 400715, China email: tangcl@swu.edu.cn |
Return to the EJDE web page