In this work we study the existence, multiplicity and concentration of positive solutions for the quasilinear problem
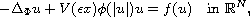
where
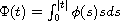 is an N-function,
is an N-function,
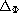 is the
is the
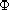 -Laplacian operator,
-Laplacian operator,
 is a
positive parameter, and
is a
positive parameter, and
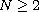 .
.
Claudianor O. Alves, Ailton R. da Silva
Abstract:
In this work we study the existence, multiplicity and concentration
of positive solutions for the quasilinear problem
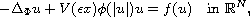
where
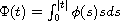 is an N-function,
is an N-function,
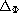 is the
is the
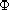 -Laplacian operator,
-Laplacian operator,
 is a
positive parameter, and
is a
positive parameter, and
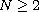 .
.
Submitted March 15, 2016. Published June 21, 2016.
Math Subject Classifications: 35A15, 35B40, 35J62, 46E30.
Key Words: Variational method; quasilinear problem, Orlicz-Sobolev space.
Show me the PDF file (340 KB), TEX file for this article.
 |
Claudianor O. Alves Universidade Federal de Campina Grande Unidade Acadêmica de Matemática - UAMat CEP: 58.429-900 - Campina Grande - PB, Brazil email: coalves@dme.ufcg.edu.br |
|---|---|
 |
Ailton R. da Silva Universidade Federal de Campina Grande Unidade Acadêmica de Matemática - UAMat CEP: 58.429-900 - Campina Grande - PB, Brazil email: ardsmat@gmail.com |
Return to the EJDE web page