In this article, we prove the multiplicity of nontrivial solutions to the critical problem with fractional Laplacian

where
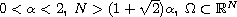 is a smooth bounded domain. More precisely, for any
is a smooth bounded domain. More precisely, for any
 ,
this problem has at least
,
this problem has at least
![$[(N+1)/2]$](gifs/ad.gif) pairs of nontrivial weak solutions.
pairs of nontrivial weak solutions.
Hui Guo
Abstract:
In this article, we prove the multiplicity of nontrivial solutions to
the critical problem with fractional Laplacian

where
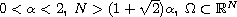 is a smooth bounded domain. More precisely, for any
is a smooth bounded domain. More precisely, for any
 ,
this problem has at least
,
this problem has at least
![$[(N+1)/2]$](gifs/ad.gif) pairs of nontrivial weak solutions.
pairs of nontrivial weak solutions.
Submitted April 9, 2016. Published June 20, 2016.
Math Subject Classifications: 35J20, 35J60, 35J67, 35R11.
Key Words: Fractional Laplacian; multiple solutions; Brezis-Nirenberg problem.
Show me the PDF file (314 KB), TEX file for this article.
 |
Hui Guo College of Mathematics and Econometrics Hunan University Changsha 410082, China email: huiguo_math@163.com |
|---|
Return to the EJDE web page