Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 147, pp. 1-14.
Ground state solutions for an asymptotically linear diffusion system
Yinbin Li, Jian Zhang
Abstract:
This article concerns the diffusion system
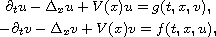
where
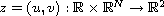 ,
,
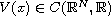 is a general periodic function, g, f
are periodic in t, x and asymptotically linear in u, v at infinity.
We find a minimizing Cerami sequence of the energy functional outside
the Nehari-Pankov manifold
is a general periodic function, g, f
are periodic in t, x and asymptotically linear in u, v at infinity.
We find a minimizing Cerami sequence of the energy functional outside
the Nehari-Pankov manifold
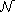 and therefore obtain ground
state solutions.
and therefore obtain ground
state solutions.
Submitted April 13, 2016. Published June 15, 2016.
Math Subject Classifications: 35J10, 35J20.
Key Words: Diffusion systems; asymptotically linear; diagonal method;
Nehari-Pankov manifold.
Show me the PDF file (275 KB),
TEX file for this article.
 |
Yinbin Li
School of Mathematics and Statistics
Central South University
Changsha, Hunan 410083, China
email: liyinbin1991@163.com
|
|---|
 |
Jian Zhang
School of Mathematics and Statistics
Hunan University of Commerce
Changsha, Hunan 410205, China
email: zhangjian433130@163.com
|
|---|
Return to the EJDE web page
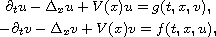
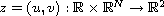 ,
,
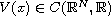 is a general periodic function, g, f
are periodic in t, x and asymptotically linear in u, v at infinity.
We find a minimizing Cerami sequence of the energy functional outside
the Nehari-Pankov manifold
is a general periodic function, g, f
are periodic in t, x and asymptotically linear in u, v at infinity.
We find a minimizing Cerami sequence of the energy functional outside
the Nehari-Pankov manifold
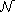 and therefore obtain ground
state solutions.
and therefore obtain ground
state solutions.

