Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 146, pp. 1-10.
Liouville-type theorems for elliptic inequalities with power
nonlinearities involving variable exponents for a fractional
Grushin operator
Mohamed Jleli, Mokhtar Kirane, Bessem Samet
Abstract:
We establish Liouville-type theorems for the elliptic inequality
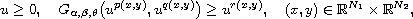
where
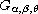 ,
,
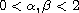 ,
,
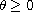 ,
is the fractional Grushin operator of mixed orders
,
is the fractional Grushin operator of mixed orders
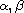 , defined by
, defined by
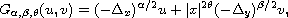
where,
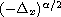 is the fractional Laplacian operator of
order
is the fractional Laplacian operator of
order
 with respect to the variable
with respect to the variable
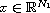 ,
and
,
and
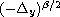 is the fractional Laplacian operator of order
is the fractional Laplacian operator of order
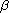 with respect to the variable
with respect to the variable
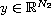 .
Here,
.
Here,
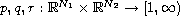 are measurable functions satisfying certain conditions.
are measurable functions satisfying certain conditions.
Submitted March 1, 2016. Published June 14, 2016.
Math Subject Classifications: 35B53, 35R11, 35J70.
Key Words: Liouville-type theorem; elliptic inequalities; variable exponent;
fractional Grushin operator.
Show me the PDF file (240 KB),
TEX file for this article.
 |
Mohamed Jleli
Department of Mathematics, College of Science
King Saud University, P.O. Box 2455
Riyadh 11451, Saudi Arabia
email: jleli@ksu.edu.sa
|
|---|
 |
Mokhtar Kirane
LaSIE, Faculté des Sciences et Technologies
Université de La Rochelle
Avenue M. Crépeau, 17042 La Rochelle, France
email: mokhtar.kirane@univ-lr.fr
|
|---|
 |
Bessem Samet
Department of Mathematics, College of Science
King Saud University, P.O. Box 2455
Riyadh 11451, Saudi Arabia
email: bsamet@ksu.edu.sa
|
|---|
Return to the EJDE web page
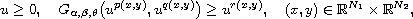
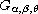 ,
,
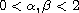 ,
,
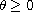 ,
is the fractional Grushin operator of mixed orders
,
is the fractional Grushin operator of mixed orders
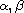 , defined by
, defined by
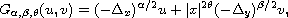
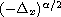 is the fractional Laplacian operator of
order
is the fractional Laplacian operator of
order
 with respect to the variable
with respect to the variable
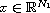 ,
and
,
and
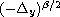 is the fractional Laplacian operator of order
is the fractional Laplacian operator of order
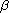 with respect to the variable
with respect to the variable
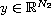 .
Here,
.
Here,
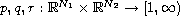 are measurable functions satisfying certain conditions.
are measurable functions satisfying certain conditions.


