In this article we consider the evolutionary
 -Laplacian equation
-Laplacian equation
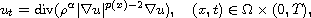
where
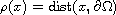 .
If the diffusion coefficient degenerates on the boundary, then
and the solution may be free from any limitations of the
boundary condition.
.
If the diffusion coefficient degenerates on the boundary, then
and the solution may be free from any limitations of the
boundary condition.
Huashui Zhan, Jie Wen
Abstract:
In this article we consider the evolutionary
 -Laplacian equation
-Laplacian equation
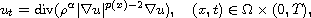
where
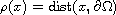 .
If the diffusion coefficient degenerates on the boundary, then
and the solution may be free from any limitations of the
boundary condition.
.
If the diffusion coefficient degenerates on the boundary, then
and the solution may be free from any limitations of the
boundary condition.
Submitted June 2, 2015. Published June 14, 2016.
Math Subject Classifications: 35L65, 35K85, 35R35.
Key Words: p(x)-Laplacian equation; diffusion coefficient;
Fichera-Oleinik theory; boundary condition; Fichera function.
Show me the PDF file (272 KB), TEX file for this article.
 |
Huashui Zhan School of Applied Mathematics Xiamen University of Technology Xiamen, Fujian 361024, China email: 2012111007@xmut.edu.cn |
|---|---|
 |
Jie Wen School of Sciences Jimei University Xiamen, Fujian 361021, China email: 1195103523@qq.com |
Return to the EJDE web page