Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 133, pp. 1-13.
Positive solutions for systems of competitive fractional
differential equations
Majda Chaieb, Abdelwaheb Dhifli, Malek Zribi
Abstract:
Using potential theory arguments, we study the existence and
boundary behavior of positive solutions in the space of weighted
continuous functions, for the fractional differential system
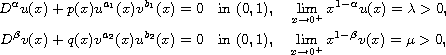
where
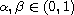 ,
,
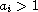 ,
,
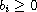 for
for
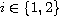 and
and
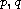 are positive continuous functions on
are positive continuous functions on
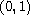 satisfying a suitable
condition relying on fractional potential properties.
satisfying a suitable
condition relying on fractional potential properties.
Submitted February 27, 2016 Published June 7, 2016.
Math Subject Classifications: 26A33, 31B25, 34A12, 34B18.
Key Words: Fractional differential system; positive solution;
potential theory; Schauder fixed point theorem.
Show me the PDF file (256 KB),
TEX file for this article.
 |
Majda Chaieb
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: majda.chaieb@gmail.com
|
|---|
 |
Abdelwaheb Dhifli
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: dhifli_waheb@yahoo.fr
|
|---|
 |
Malek Zribi
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: malek.zribi@insat.rnu.tn
|
|---|
Return to the EJDE web page
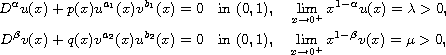
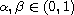 ,
,
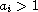 ,
,
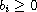 for
for
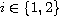 and
and
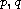 are positive continuous functions on
are positive continuous functions on
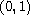 satisfying a suitable
condition relying on fractional potential properties.
satisfying a suitable
condition relying on fractional potential properties.


