Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 132, pp. 1-14.
Perturbation of the free boundary in elliptic problem with discontinuities
Sabri Bensid
Abstract:
We study the discontinuous elliptic problem
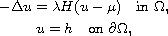
where
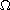 is a regular bounded domain of
is a regular bounded domain of
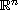 ,
,
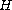 is the Heaviside function,
is the Heaviside function,
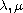 are a positive real parameters
and h is a given function. We prove the existence of solutions,
and characterize the free boundaries
are a positive real parameters
and h is a given function. We prove the existence of solutions,
and characterize the free boundaries
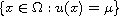 using the perturbation of the boundary condition and smooth
boundary of the domain.
using the perturbation of the boundary condition and smooth
boundary of the domain.
Submitted April 14, 2016. Published June 7, 2016.
Math Subject Classifications: 34R35, 35J25.
Key Words: Perturbation; implicit function theorem; free boundary problem.
Show me the PDF file (243 KB),
TEX file for this article.
 |
Sabri Bensid
Department of Mathematics
Faculty of Sciences
University of Tlemcen, B.P. 119
Tlemcen 13000, Algeria
email: edp_sabri@yahoo.fr
|
|---|
Return to the EJDE web page
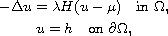
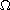 is a regular bounded domain of
is a regular bounded domain of
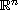 ,
,
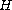 is the Heaviside function,
is the Heaviside function,
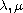 are a positive real parameters
and h is a given function. We prove the existence of solutions,
and characterize the free boundaries
are a positive real parameters
and h is a given function. We prove the existence of solutions,
and characterize the free boundaries
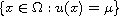 using the perturbation of the boundary condition and smooth
boundary of the domain.
using the perturbation of the boundary condition and smooth
boundary of the domain.
