Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 130, pp. 1-7.
Uniqueness of a positive solution for quasilinear elliptic equations
in Heisenberg group
Kaushik Bal
Abstract:
In this note we address the question of uniqueness of the Brezis-Oswald
problem for the p-Laplacian operator in Heisenberg Group. The non-availability
of
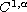 regularity for all
regularity for all
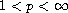 is the problem to extend
the proof of Diaz-Saa [10] in the Heisenberg Group case. We overcome
the problem by proving directly a generalized version of Diaz-Saa inequality
in the Heisenberg Group.
is the problem to extend
the proof of Diaz-Saa [10] in the Heisenberg Group case. We overcome
the problem by proving directly a generalized version of Diaz-Saa inequality
in the Heisenberg Group.
Submitted January 18, 20016. Published June 6, 2016.
Math Subject Classifications: 35R03, 35J92, 35J70.
Key Words: Quasilinear elliptic equation; Picone's identity; Heisenberg group.
Show me the PDF file (202 KB),
TEX file for this article.
Kaushik Bal
Department of Mathematics and Statistics
Indian Institute of Technology
Kanpur, Uttar Pradesh-280016 India
email: kaushik@iitk.ac.in
|
Return to the EJDE web page
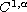 regularity for all
regularity for all
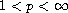 is the problem to extend
the proof of Diaz-Saa [10] in the Heisenberg Group case. We overcome
the problem by proving directly a generalized version of Diaz-Saa inequality
in the Heisenberg Group.
is the problem to extend
the proof of Diaz-Saa [10] in the Heisenberg Group case. We overcome
the problem by proving directly a generalized version of Diaz-Saa inequality
in the Heisenberg Group.