This article concerns the Cauchy problem associated with the nonlinear fourth-order Schrodinger equation with isotropic and anisotropic mixed dispersion. This model is given by the equation
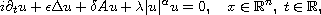
where A is either the operator
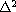 (isotropic dispersion)
or
(isotropic dispersion)
or
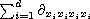 ,
,
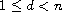 (anisotropic dispersion), and
(anisotropic dispersion), and
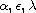 are real
parameters. We obtain local and global well-posedness results in
spaces of initial data with low regularity, based on weak-
are real
parameters. We obtain local and global well-posedness results in
spaces of initial data with low regularity, based on weak-
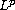 spaces.
Our analysis also includes the biharmonic and anisotropic biharmonic
equation
spaces.
Our analysis also includes the biharmonic and anisotropic biharmonic
equation
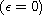 ; in this case, we obtain the existence of
self-similar solutions because of their scaling invariance property.
In a second part, we analyze the convergence of solutions for the
nonlinear fourth-order Schrodinger equation
; in this case, we obtain the existence of
self-similar solutions because of their scaling invariance property.
In a second part, we analyze the convergence of solutions for the
nonlinear fourth-order Schrodinger equation
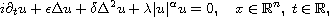
as
 approaches zero, in the
approaches zero, in the
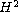 -norm,
to the solutions of
the corresponding biharmonic equation
-norm,
to the solutions of
the corresponding biharmonic equation
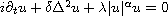 .
.

