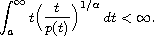Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 129, pp. 1-32.
Asymptotic behavior of intermediate solutions of fourth-order nonlinear
differential equations with regularly varying coefficients
Aleksandra B. Trajkovic, Jelena V. Manojlovic
Abstract:
We study the fourth-order nonlinear differential equation

with regularly varying coefficient
 satisfying
satisfying
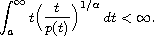
in the framework of regular variation. It is shown that complete information
can be acquired about the existence of all possible intermediate regularly
varying solutions and their accurate asymptotic behavior at infinity.
Submitted March 26, 2016. Published June 5, 2016.
Math Subject Classifications: 34C11, 34E05, 26A12.
Key Words: Fourth order differential equation; asymptotic behavior of solutions;
positive solution, regularly varying solution, slowly varying solution.
Show me the PDF file (440 KB),
TEX file for this article.
 |
Aleksandra Trajkovic
University of Nis
Faculty of Science and Mathematics
Department of Mathematics
Visegradska 33, 18000 Nis, Serbia
email: aleksandra.trajkovic@pmf.edu.rs
|
|---|
 |
Jelena V. Manojlovic
University of Nis
Faculty of Science and Mathematics
Department of Mathematics
Visegradska 33, 18000 Nis, Serbia
email: jelenam@pmf.ni.ac.rs
|
|---|
Return to the EJDE web page

 satisfying
satisfying