Electron. J. Diff. Equ., Vol. 2016 (2016), No. 122, pp. 1-12.

Limit cycles for $\mathbb{Z}_{2n}$-equivariant systems without infinite equilibria

Isabel S. Labouriau, Adrian C. Murza

Abstract:
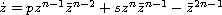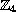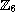We analyze the dynamics of a class of $\mathbb{Z}_{2n}$-equivariant differential equations of the form $\dot{z}=pz^{n-1}\bar{z}^{n-2}+sz^{n}\bar{z}^{n-1}-\bar{z}^{2n-1}$, where z is complex, the time t is real, while p and s are complex parameters. This study is the generalisation to $\mathbb{Z}_{2n}$ of previous works with $\mathbb{Z}_4$ and $\mathbb{Z}_6$ symmetry. We reduce the problem of finding limit cycles to an Abel equation, and provide criteria for proving in some cases uniqueness and hyperbolicity of the limit cycle that surrounds either 1, 2n+1 or 4n+1 equilibria, the origin being always one of these points.

Submitted October 10, 2015. Published May 16, 2016.
Math Subject Classifications: 34C07, 34C14, 34C23, 37C27
Key Words: Planar autonomous ordinary differential equations; limit cycles; symmetric polynomial systems.

Show me the PDF file (361 KB), TEX file for this article.

Isabel S. Labouriau
Centro de Matemática da Universidade do Porto
Rua do Campo Alegre 687
4169-007 Porto, Portugal
email: islabour@fc.up.pt
Adrian C. Murza
Centro de Matemática da Universidade do Porto
Rua do Campo Alegre 687
4169-007 Porto, Portugal
email: adrian_murza@hotmail.com

Return to the EJDE web page