Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 114, pp. 1-14.
Radial solutions with a prescribed number of zeros for a superlinear
Dirichlet problem in annular domain
Boubker Azeroual, Abderrahim Zertiti
Abstract:
In this article we study the existence of radially symmetric solutions
to a superlinear Dirichlet problem in annular domain in
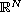 .
Using fairly straightforward tools of the theory of ordinary differential
equations, we show that if k is a sufficiently large nonnegative integer,
there is a solution u which has exactly (k-1) interior zeros.
.
Using fairly straightforward tools of the theory of ordinary differential
equations, we show that if k is a sufficiently large nonnegative integer,
there is a solution u which has exactly (k-1) interior zeros.
Submitted February 4, 2016. Published May 3, 2016.
Math Subject Classifications: 35J25, 35B05, 35A24.
Key Words: Superlinear; radial solution; Bessel's equation.
Show me the PDF file (250 KB),
TEX file for this article.
 |
Azeroual Boubker
Université Abdelmalek Essaadi
Faculté des sciences
Département de Mathématiques
BP 2121, Tetouan, Morocco
email: boubker_azeroual@yahoo.fr
|
|---|
 |
Abderrahim Zertiti
Université Abdelmalek Essaadi
Faculté des sciences
Département de Mathématiques
BP 2121, Tetouan, Morocco
email: abdzertiti@hotmail.fr
|
|---|
Return to the EJDE web page
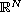 .
Using fairly straightforward tools of the theory of ordinary differential
equations, we show that if k is a sufficiently large nonnegative integer,
there is a solution u which has exactly (k-1) interior zeros.
.
Using fairly straightforward tools of the theory of ordinary differential
equations, we show that if k is a sufficiently large nonnegative integer,
there is a solution u which has exactly (k-1) interior zeros.

