Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 104, pp. 1-13.
Long time decay for 3D Navier-Stokes equations in Sobolev-Gevrey spaces
Jamel Benameur, Lotfi Jlali
Abstract:
In this article, we study the long time decay of global solution to
3D incompressible Navier-Stokes equations. We prove
that if
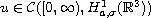 is a global solution, where
is a global solution, where
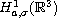 is the Sobolev-Gevrey
spaces with parameters a>0 and
is the Sobolev-Gevrey
spaces with parameters a>0 and
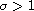 ,
then
,
then
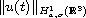 decays to zero as time approaches
infinity. Our technique is based on Fourier analysis.
decays to zero as time approaches
infinity. Our technique is based on Fourier analysis.
Submitted February 2, 2016. Published April 21, 2016.
Math Subject Classifications: 35Q30, 35D35.
Key Words: Navier-Stokes Equation; critical spaces; long time decay.
Show me the PDF file (234 KB),
TEX file for this article.
 |
Jamel Benameur
Institut Supérieur des Sciences Appliquées
et de Technologie de Gabès
Université de Gabès, Tunisia
email: jamelbenameur@gmail.com
|
|---|
 |
Lotfi Jlali
Faculté de Sciences Mathématiques,
Physiques et Naturelles de Tunis
Université de Tunis
El Manar, Tunisia
email: lotfihocin@gmail.com
|
|---|
Return to the EJDE web page
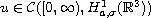 is a global solution, where
is a global solution, where
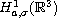 is the Sobolev-Gevrey
spaces with parameters a>0 and
is the Sobolev-Gevrey
spaces with parameters a>0 and
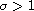 ,
then
,
then
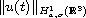 decays to zero as time approaches
infinity. Our technique is based on Fourier analysis.
decays to zero as time approaches
infinity. Our technique is based on Fourier analysis.

