Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 102, pp. 1-22.
Nontrivial solutions for Kirchhoff equations with periodic potentials
Xiaoyan Ma, Xiaoming He
Abstract:
In this article we consider the Kirchhoff equations
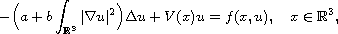
where
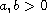 are constants, the nonlinearity f is superlinear
at infinity with subcritical or critical growth and V is positive,
continuous and periodic in x. Some existence results for
ground state solutions are obtained by using variational methods.
Moreover, when
are constants, the nonlinearity f is superlinear
at infinity with subcritical or critical growth and V is positive,
continuous and periodic in x. Some existence results for
ground state solutions are obtained by using variational methods.
Moreover, when
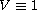 we obtain ground state solutions for the
above problem with a wide class of superlinear nonlinearities by
using a new approach.
we obtain ground state solutions for the
above problem with a wide class of superlinear nonlinearities by
using a new approach.
Submitted March 28, 2016. Published April 20, 2016.
Math Subject Classifications: 47G20, 35J50, 35B65.
Key Words: Kirchhoff-type problems; ground states; Nehari manifold;
critical Sobolev exponent.
Show me the PDF file (338 KB),
TEX file for this article.
 |
Xiaoyan Ma
College of Science
Minzu University of China
Beijing 100081, China
email: SX140963@muc.edu.cn
|
|---|
 |
Xiaoming He
College of Science
Minzu University of China
Beijing 100081, China
email: xmhe923@muc.edu.cn
|
|---|
Return to the EJDE web page
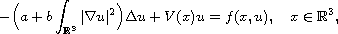
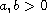 are constants, the nonlinearity f is superlinear
at infinity with subcritical or critical growth and V is positive,
continuous and periodic in x. Some existence results for
ground state solutions are obtained by using variational methods.
Moreover, when
are constants, the nonlinearity f is superlinear
at infinity with subcritical or critical growth and V is positive,
continuous and periodic in x. Some existence results for
ground state solutions are obtained by using variational methods.
Moreover, when
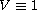 we obtain ground state solutions for the
above problem with a wide class of superlinear nonlinearities by
using a new approach.
we obtain ground state solutions for the
above problem with a wide class of superlinear nonlinearities by
using a new approach.

