Electron. J. Diff. Equ., Vol. 2016 (2016), No. 10, pp. 1-19.

Multiple solutions for quasilinear elliptic equations with sign-changing potential

Ruimeng Wang, Kun Wang, Kaimin Teng

Abstract:
In this article, we study the quasilinear elliptic equation
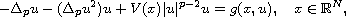
$$ -\Delta_{p} u-(\Delta_{p}u^{2})u+ V (x)|u|^{p-2}u=g(x,u), \quad x\in \mathbb{R}^N, $$
where the potential V(x) and the nonlinearity g(x,u) are allowed to be sign-changing. Under some suitable assumptions on V and g, we obtain the multiplicity of solutions by using minimax methods.

Submitted July 8, 2015. Published January 6, 2016.
Math Subject Classifications: 35B38, 35D05, 35J20.
Key Words: Quasilinear Schrodinger equation; symmetric mountain pass theorem; Cerami condition.

Show me the PDF file (302 KB), TEX file for this article.

Ruimeng Wang
Department of Mathematics
Taiyuan University of Technology
Taiyuan, Shanxi 030024, China
email: wangruimeng112779@163.com
Kun Wang
Department of Mathematics
Taiyuan University of Technology
Taiyuan, Shanxi 030024, China
email: windwk0608@163.com
Kaimin Teng
Department of Mathematics
Taiyuan University of Technology
Taiyuan, Shanxi 030024, China
email: tengkaimin2013@163.com

Return to the EJDE web page