Electron. J. Diff. Equ.,
Vol. 2016 (2016), No. 06, pp. 1-8.
Monotone iterative method for fractional differential equations
Zhanbing Bai, Shuo Zhang, Sujing Sun, Chun Yin
Abstract:
In this article, by using the lower and upper solution method,
we prove the existence of iterative solutions for a class of fractional
initial value problem with non-monotone term

where
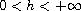 ,
,
![$f\in C([0, h]\times \mathbb{R}, \mathbb{R})$](gifs/ac.gif) ,
,
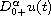 is the standard Riemann-Liouville fractional
derivative,
is the standard Riemann-Liouville fractional
derivative,
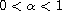 .
A new condition on the nonlinear
term is given to guarantee the equivalence between the solution of the
IVP and the fixed-point of the corresponding operator.
Moreover, we show the existence of maximal and minimal solutions.
.
A new condition on the nonlinear
term is given to guarantee the equivalence between the solution of the
IVP and the fixed-point of the corresponding operator.
Moreover, we show the existence of maximal and minimal solutions.
Submitted October 14, 2015. Published January 6, 2016.
Math Subject Classifications: 34B15, 34A08.
Key Words: Fractional initial value problem; lower and upper solution method;
existence of solutions.
Show me the PDF file (206 KB),
TEX file for this article.
 |
Zhanbing Bai
College of Mathematics and System Science
Shandong University of Science and Technology
Qingdao 266590, China
email: zhanbingbai@163.com
|
|---|
 |
Shuo Zhang
College of Mathematics and System Science
Shandong University of Science and Technology
Qingdao 266590, China
email: 18353250431@163.com
|
|---|
 |
Sujing Sun
College of Information Science and Engineering
Shandong University of Science and Technology
Qingdao 266590, China
email: kdssj@163.com
|
|---|
 |
Chun Yin
School of Automation Engineering
University of Electronic Science and Technology of China
Chengdu 611731, China
email: yinchun.86416@163.com
|
|---|
Return to the EJDE web page

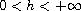 ,
,
![$f\in C([0, h]\times \mathbb{R}, \mathbb{R})$](gifs/ac.gif) ,
,
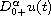 is the standard Riemann-Liouville fractional
derivative,
is the standard Riemann-Liouville fractional
derivative,
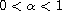 .
A new condition on the nonlinear
term is given to guarantee the equivalence between the solution of the
IVP and the fixed-point of the corresponding operator.
Moreover, we show the existence of maximal and minimal solutions.
.
A new condition on the nonlinear
term is given to guarantee the equivalence between the solution of the
IVP and the fixed-point of the corresponding operator.
Moreover, we show the existence of maximal and minimal solutions.



