In this article, we consider the nonlocal problem
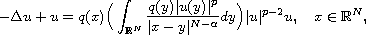
where
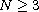 ,
,
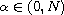 ,
,
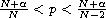 and q(x) is a given potential. Under suitable assumptions on q(x),
we prove the existence and nonexistence of nontrivial solutions.
and q(x) is a given potential. Under suitable assumptions on q(x),
we prove the existence and nonexistence of nontrivial solutions.
Tao Wang
Abstract:
In this article, we consider the nonlocal problem
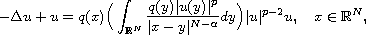
where
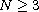 ,
,
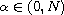 ,
,
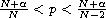 and q(x) is a given potential. Under suitable assumptions on q(x),
we prove the existence and nonexistence of nontrivial solutions.
and q(x) is a given potential. Under suitable assumptions on q(x),
we prove the existence and nonexistence of nontrivial solutions.
Submitted November 8, 2015. Published January 4, 2016.
Math Subject Classifications: 35A15, 35J20, 35J60.
Key Words: Choquard equation; nonlocal nonlinearities; variational methods.
Show me the PDF file (310 KB), TEX file for this article.
 |
Tao Wang School of Mathematics and Statistics Central South University Changsha, Hunan 410083, China email: wt_61003@163.com |
|---|
Return to the EJDE web page