Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 95, pp. 1-9.
An extension of the Lax-Milgram theorem and its
application to fractional differential equations
Nemat Nyamoradi, Mohammad Rassol Hamidi
Abstract:
In this article, using an iterative technique, we introduce an
extension of the Lax-Milgram theorem which can be used for proving
the existence of solutions to boundary-value problems.
Also, we apply of the obtained result to the
fractional differential equation
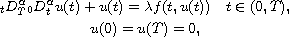
where
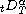 and
and
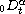 are the right and
left Riemann-Liouville fractional derivative of order
are the right and
left Riemann-Liouville fractional derivative of order
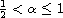 respectively,
respectively,
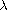 is a parameter and
is a parameter and
![$f:[0,T]\times\mathbb{R}\to\mathbb{R}$](gifs/af.gif) is a continuous function. Applying a regularity argument to this
equation, we show that every weak solution is a classical solution.
is a continuous function. Applying a regularity argument to this
equation, we show that every weak solution is a classical solution.
Submitted February 1, 2015. Published April 13, 2015.
Math Subject Classifications: 34A08, 35A15, 35B38.
Key Words: Lax-Milgram theorem; fractional differential equation.
Show me the PDF file (216 KB),
TEX file, and other files for this article.
 |
Nemat Nyamoradi
Department of Mathematics, Faculty of Sciences
Razi University, 67149 Kermanshah, Iran
email: nyamoradi@razi.ac.ir, neamat80@yahoo.com
|
|---|
 |
Mohammad Rassol Hamidi
Department of Mathematics, Faculty of Sciences
Razi University, 67149 Kermanshah, Iran
email: mohammadrassol.hamidi@yahoo.com
|
|---|
Return to the EJDE web page
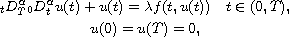
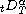 and
and
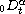 are the right and
left Riemann-Liouville fractional derivative of order
are the right and
left Riemann-Liouville fractional derivative of order
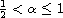 respectively,
respectively,
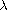 is a parameter and
is a parameter and
![$f:[0,T]\times\mathbb{R}\to\mathbb{R}$](gifs/af.gif) is a continuous function. Applying a regularity argument to this
equation, we show that every weak solution is a classical solution.
is a continuous function. Applying a regularity argument to this
equation, we show that every weak solution is a classical solution.

