Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 93, pp. 1-14.
Existence of solutions for fractional p-Kirchhoff equations
with critical nonlinearities
Pawan Kumar Mishra, Konijeti Sreenadh
Abstract:
In this article, we show the existence of non-negative solutions of the
fractional p-Kirchhoff problem

where
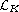 is a p-fractional type non local operator with kernel K,
is a p-fractional type non local operator with kernel K,
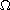 is a bounded domain in
is a bounded domain in
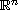 with smooth boundary,
M and f are continuous functions, and
with smooth boundary,
M and f are continuous functions, and
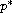 is the fractional Sobolev exponent.
is the fractional Sobolev exponent.
Submitted September 2, 2014. Published April 12, 2015.
Math Subject Classifications: 34B27, 35J60, 35B05.
Key Words: Kirchhoff non-local operators; fractional differential equations;
critical exponent.
Show me the PDF file (274 KB),
TEX file, and other files for this article.
 |
Pawan Kumar Mishra
Department of Mathematics
Indian Institute of Technology Delhi
Hauz Khaz, New Delhi-16, India
email: pawanmishra31284@gmail.com
|
|---|
 |
Konijeti Sreenadh
Department of Mathematics
Indian Institute of Technology Delhi
Hauz Khaz, New Delhi-16, India
email: sreenadh@gmail.com
|
|---|
Return to the EJDE web page

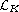 is a p-fractional type non local operator with kernel K,
is a p-fractional type non local operator with kernel K,
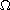 is a bounded domain in
is a bounded domain in
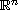 with smooth boundary,
M and f are continuous functions, and
with smooth boundary,
M and f are continuous functions, and
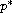 is the fractional Sobolev exponent.
is the fractional Sobolev exponent.

