Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 85, pp. 1-18.
Ground states for a modified capillary surface equation
in weighted Orlicz-Sobolev space
Guoqing Zhang, Huiling Fu
Abstract:
In this article, we prove a compact embedding theorem for the weighted
Orlicz-Sobolev space of radially symmetric functions. Using the embedding
theorem and critical points theory, we prove the existence of multiple
radial solutions and radial ground states for the following modified capillary
surface equation
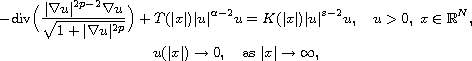
where
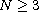 ,
,
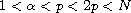 ,
,
 satisfies some suitable conditions,
satisfies some suitable conditions,
 and
and
 are continuous, nonnegative functions.
are continuous, nonnegative functions.
Submitted August 6, 2014. Published March 7, 2015.
Math Subject Classifications: 35J65, 35J70.
Key Words: Compact theorem; modified capillary surface equation;
weighted Orlicz-Sobolev space; ground state.
Show me the PDF file (297 KB),
TEX file, and other files for this article.
 |
Guoqing Zhang
College of Sciences
University of Shanghai for Science and Technology
Shanghai 200093, China
email: shzhangguoqing@126.com
|
|---|
 |
Huiling Fu
College of Sciences
University of Shanghai for Science and Technology
Shanghai 200093, China
email: fuhuiliing80@163.com
|
|---|
Return to the EJDE web page
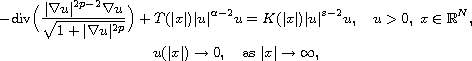
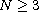 ,
,
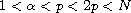 ,
,
 satisfies some suitable conditions,
satisfies some suitable conditions,
 and
and
 are continuous, nonnegative functions.
are continuous, nonnegative functions.

