Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 78, pp. 1-11.
Multiple positive solutions for elliptic problem with concave
and convex nonlinearities
Jiayin Liu, Lin Zhao, Peihao Zhao
Abstract:
In this article, we consider the existence of multiple solutions to
the elliptic problem
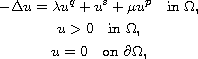
where
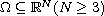 is a bounded domain with
smooth boundary
is a bounded domain with
smooth boundary
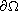 ,
,
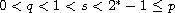 ,
,
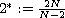 ,
,
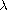 and
and
 are nonnegative parameters. By using variational methods,
truncation and Moser iteration techniques, we show that if the parameters
are nonnegative parameters. By using variational methods,
truncation and Moser iteration techniques, we show that if the parameters
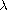 and
and
 are small enough, then the problem has at least two
positive solutions.
are small enough, then the problem has at least two
positive solutions.
Submitted November 27, 2014. Published March 31, 2015.
Math Subject Classifications: 35J20, 35J25, 35J60.
Key Words: Variational methods; supercritical exponent;
mountain pass theorem, Moser iteration technique.
Show me the PDF file (246 KB),
TEX file, and other files for this article.
 |
Jiayin Liu
School of Mathematics and Statistics, Lanzhou University
Lanzhou, Gansu 730000, China
email: xecd@163.com
|
|---|
 |
Lin Zhao
Department of Mathematics
China University of Mining and Technology
Xuzhou, Jiangsu 221116, China
email: zhaolinmath@gmail.com
|
|---|
 |
Peihao Zhao
School of Mathematics and Statistics
Lanzhou University
Lanzhou, Gansu 730000, China
email: zhaoph@lzu.edu.cn
|
|---|
Return to the EJDE web page
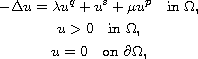
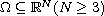 is a bounded domain with
smooth boundary
is a bounded domain with
smooth boundary
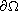 ,
,
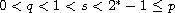 ,
,
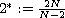 ,
,
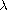 and
and
 are nonnegative parameters. By using variational methods,
truncation and Moser iteration techniques, we show that if the parameters
are nonnegative parameters. By using variational methods,
truncation and Moser iteration techniques, we show that if the parameters
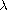 and
and
 are small enough, then the problem has at least two
positive solutions.
are small enough, then the problem has at least two
positive solutions.


