Electron. J. Diff. Equ., Vol. 2015 (2015), No. 76, pp. 1-28.

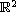
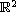
Mixed interior and boundary peak solutions of the Neumann problem for the Henon equation in $\mathbb{R}^2$

Yibin Zhang, Haitao Yang

Abstract:
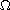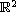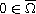Let $\Omega$ be a bounded domain in $\mathbb{R}^2$ with smooth boundary and $0\in\overline{\Omega}$, we study the Neumann problem for the Henon equation
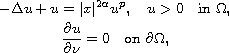
$$\displaylines{ -\Delta u+u=|x|^{2\alpha}u^p,\quad u>0 \quad \text{in } \Omega,\cr \frac{\partial u}{\partial\nu}=0\quad \text{on } \partial\Omega, }$$
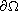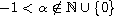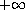where $\nu$ denotes the outer unit normal vector to $\partial\Omega$, $-1<\alpha\not\in\mathbb{N}\cup\{0\}$ and p is a large exponent. In a constructive way, we show that, as p approaches $+\infty$, such a problem has a family of positive solutions with arbitrarily many interior and boundary spikes involving the origin. The same techniques lead also to a more general result on Henon-type weights.

Submitted October 14, 2014. Published March 26, 2015.
Math Subject Classifications: 35J25, 35J20, 58K05.
Key Words: Mixed interior and boundary peak solutions; Henon-type weight; large exponent; Lyapunov-Schmidt reduction process.

Show me the PDF file (404 KB), TEX file, and other files for this article.

Yibin Zhang
College of Sciences, Nanjing Agricultural University
Nanjing 210095, China
email: yibin10201029@njau.edu.cn
  Haitao Yang
Department of Mathematics, Zhejiang University
Hangzhou 310027, China
email: htyang@css.zju.edu.cn

Return to the EJDE web page