Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 68, pp. 1-12.
Oscillation of arbitrary-order derivatives of solutions to linear
differential equations taking small functions in the unit disc
Pan Gong, Li-Peng Xiao
Abstract:
In this article, we study the relationship between solutions and
their derivatives of the differential equation
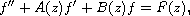
where
 are meromorphic functions of finite iterated
p-order in the unit disc.
We obtain some oscillation theorems for
are meromorphic functions of finite iterated
p-order in the unit disc.
We obtain some oscillation theorems for
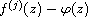 ,
where f is a solution and
,
where f is a solution and
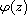 is a small function.
is a small function.
Submitted January 6, 2015. Published March 20, 2015.
Math Subject Classifications: 34M10, 30D35.
Key Words: Unit disc; iterated order; growth; exponent of convergence.
Show me the PDF file (236 KB),
TEX file, and other files for this article.
 |
Pan Gong
Institute of Mathematics and Information Science
Jiangxi Normal University
Nanchang 330022, China
email: gongpan12@163.com
|
|---|
 |
Li Peng Xiao
Institute of Mathematics and Information Science
Jiangxi Normal University
Nanchang 330022, China
email: 2992507211@qq.com
|
|---|
Return to the EJDE web page
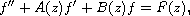
 are meromorphic functions of finite iterated
p-order in the unit disc.
We obtain some oscillation theorems for
are meromorphic functions of finite iterated
p-order in the unit disc.
We obtain some oscillation theorems for
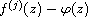 ,
where f is a solution and
,
where f is a solution and
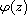 is a small function.
is a small function.

