Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 62, pp. 1-9.
Blow-up criterion for the zero-diffusive Boussinesq equations
via the velocity components
Weihua Wang
Abstract:
This article concerns the blow up for the smooth solutions of the
three-dimensional Boussinesq equations with zero diffusivity.
It is shown that if any two components of the velocity field u
satisfy
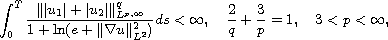
then the local smooth solution
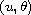 can be continuously
extended to
can be continuously
extended to
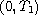 for some
for some
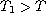 .
.
Submitted September 29, 2014. Published March 11, 2015.
Math Subject Classifications: 35Q35, 76D05.
Key Words: Zero-diffusive Boussinesq equations; blow up criterion;
Lorentz spaces.
Show me the PDF file (214 KB),
TEX file, and other files for this article.
 |
Weihua Wang
School of Mathematics and Statistics
Hubei University, Wuhan 430062, China
email: wwh73@hubu.edu.cn
|
|---|
Return to the EJDE web page
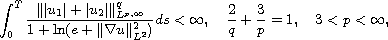
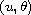 can be continuously
extended to
can be continuously
extended to
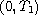 for some
for some
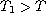 .
.
