Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 61, pp. 1-16.
Large time behavior for p(x)-Laplacian equations with irregular data
Xiaojuan Chai, Haisheng Li, Weisheng Niu
Abstract:
We study the large time behavior of solutions to p(x)-Laplacian
equations with irregular data. Under proper assumptions, we show that
the entropy solution of parabolic p(x)-Laplacian equations converges
in
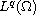 to the unique stationary entropy solution as t
tends to infinity.
to the unique stationary entropy solution as t
tends to infinity.
Submitted November 24, 2014. Published March 11, 2015.
Math Subject Classifications: 35B40, 35K55.
Key Words: p(x)-Laplacian equation; large time behavior; irregular data.
Show me the PDF file (290 KB),
TEX file, and other files for this article.
 |
Xiaojuan Chai
School of Mathematical Sciences
Anhui University,
Hefei, China
email: chaixj@ahu.edu.cn
|
|---|
 |
Haisheng Li
School of Mathematical Sciences
Anhui University,
Hefei 230601, China
email: squeensy@sina.com
|
|---|
 |
Weisheng Niu
School of Mathematical Sciences
Anhui University,
Hefei 230601, China
email: niuwsh@ahu.edu.cn
|
|---|
Return to the EJDE web page
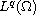 to the unique stationary entropy solution as t
tends to infinity.
to the unique stationary entropy solution as t
tends to infinity.


