Soonsik Kwon, Shuanglin Shao
Abstract:
We consider the global dynamics of the defocusing generalized KdV equation
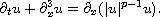
We use Tao's theorem [5] that the energy moves faster than the
mass to prove a moment type dispersion estimate. As an application of
the dispersion estimate, we show that there is no soliton-like solutions
with a certain decaying assumption.
Submitted May 21, 2013. Published February 24, 2015.
Math Subject Classifications: 35Q53.
Key Words: Generalized KdV equation; soliton, scattering.
Show me the PDF file (181 KB), TEX file, and other files for this article.
 |
Soonsik Kwon Department of Mathematical Sciences Korea Advanced Institute of Science and Technology 291 Daehak-ro Yuseong-gu, Daejeon 305-701, Korea email: soonsikk@kaist.edu |
|---|---|
 |
Shuanglin Shao Department of Mathematics, University of Kansas Lawrence, KS 66045, USA email: slshao@math.ku.edu |
Return to the EJDE web page