Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 33, pp. 1-19.
Mathematical analysis for an age-structured HIV infection model
with saturation infection rate
Jinliang Wang, Ran Zhang, Toshikazu Kuniya
Abstract:
In this article, we study a continuous age-structured HIV infection model.
For the case of the saturation infection rate, the basic reproduction number
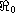 is shown to be a sharp threshold value for the global dynamics;
that is, the infection-free equilibrium is globally stable if
is shown to be a sharp threshold value for the global dynamics;
that is, the infection-free equilibrium is globally stable if
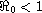 ,
while a unique infection equilibrium is so if
,
while a unique infection equilibrium is so if
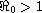 .
For the proof, we use Lyapunov functional techniques based on the relative
compactness of the orbit and uniform persistence of the system.
.
For the proof, we use Lyapunov functional techniques based on the relative
compactness of the orbit and uniform persistence of the system.
Submitted April 25, 2014. Published February 6, 2015.
Math Subject Classifications: 92D30, 34D23, 34K20.
Key Words: Age-infection model; nonlinear incidence rate;
relative compactness; uniform persistence; Lyapunov function.
Show me the PDF file (286 KB),
TEX file, and other files for this article.
 |
Jinliang Wang
School of Mathematical Science
Heilongjiang University
Harbin 150080, China
email: jinliangwang@hlju.edu.cn
|
|---|
 |
Ran Zhang
School of Mathematical Science
Heilongjiang University
Harbin 150080, China
email: ranzhang90@aliyun.com
|
|---|
 |
Toshikazu Kuniya
Graduate School of System Informatics
Kobe University, 1-1 Rokkodai-cho
Nada-ku, Kobe 657-8501, Japan
email: tkuniya@port.kobe-u.ac.jp
|
|---|
Return to the EJDE web page
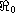 is shown to be a sharp threshold value for the global dynamics;
that is, the infection-free equilibrium is globally stable if
is shown to be a sharp threshold value for the global dynamics;
that is, the infection-free equilibrium is globally stable if
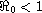 ,
while a unique infection equilibrium is so if
,
while a unique infection equilibrium is so if
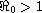 .
For the proof, we use Lyapunov functional techniques based on the relative
compactness of the orbit and uniform persistence of the system.
.
For the proof, we use Lyapunov functional techniques based on the relative
compactness of the orbit and uniform persistence of the system.


