Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 313, pp. 1-11.
Existence of solutions to second-order nonlinear coupled systems
with nonlinear coupled boundary conditions
Imran Talib, Naseer Ahmad Asif, Cemil Tunc
Abstract:
In this article, study the existence of solutions for the second-order
nonlinear coupled system of ordinary differential equations
![$$\displaylines{
u''(t)=f(t,v(t)),\quad t\in [0,1],\cr
v''(t)=g(t,u(t)),\quad t\in [0,1],
}$$](gifs/aa.gif)
with nonlinear coupled boundary conditions
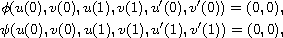
where
![$f,g:[0,1]\times \mathbb{R}\to \mathbb{R}$](gifs/ac.gif) and
and
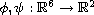 are continuous functions.
Our main tools are coupled lower and upper solutions, Arzela-Ascoli
theorem, and Schauder's fixed point theorem.
are continuous functions.
Our main tools are coupled lower and upper solutions, Arzela-Ascoli
theorem, and Schauder's fixed point theorem.
Submitted July 14, 2015. Published December 24, 2015.
Math Subject Classifications: 34B10, 34B15.
Key Words: Lower and upper solutions; coupled system;
coupled boundary conditions; Arzela-Ascoli theorem;
Schauder's fixed point theorem.
Show me the PDF file (221 KB),
TEX file, and other files for this article.
 |
Imran Talib
Department of Mathematics, School of Science
University of Management and Technology
CII Johar Town, Lahore, Pakistan
email: imrantaalib@gmail.com
|
|---|
 |
Naseer Ahmad Asif
Department of Mathematics, School of Science
University of Management and Technology
CII Johar Town, Lahore, Pakistan
email: naseerasif@yahoo.com
|
|---|
 |
Cemil Tunc
Department of Mathematics Faculty of Sciences
Yuzuncu Yil University, Van - Turkey
email: cemtunc@yahoo.com
|
|---|
Return to the EJDE web page
![$$\displaylines{
u''(t)=f(t,v(t)),\quad t\in [0,1],\cr
v''(t)=g(t,u(t)),\quad t\in [0,1],
}$$](gifs/aa.gif)
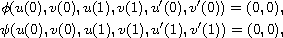
![$f,g:[0,1]\times \mathbb{R}\to \mathbb{R}$](gifs/ac.gif) and
and
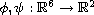 are continuous functions.
Our main tools are coupled lower and upper solutions, Arzela-Ascoli
theorem, and Schauder's fixed point theorem.
are continuous functions.
Our main tools are coupled lower and upper solutions, Arzela-Ascoli
theorem, and Schauder's fixed point theorem.


