Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 312, pp. 1-10.
Nonexistence of non-trivial global weak solutions for higher-order
nonlinear Schrodinger equations
Abderrazak Nabti
Abstract:
We study the initial-value problem for the higher-order nonlinear
Schrodinger equation
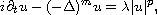
subject to the initial data
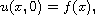
where
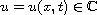 is a complex-valued function,
is a complex-valued function,
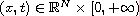 ,
,
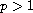 ,
,
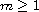 ,
,
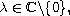 and
and
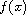 is a given complex-valued function. We prove nonexistence of
a nontrivial global weak solution. Furthermore, we prove that
the
is a given complex-valued function. We prove nonexistence of
a nontrivial global weak solution. Furthermore, we prove that
the
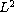 -norm
of the local in time
-norm
of the local in time
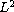 -solution blows
up at a finite time.
-solution blows
up at a finite time.
Submitted October 20, 2015. Published December 21, 2015.
Math Subject Classifications: 35Q55.
Key Words: Nonlinear Schrodinger equation; global solution; blowup.
Show me the PDF file (248 KB),
TEX file, and other files for this article.
 |
Abderrazak Nabti
Laboratoire de Mathématiques, Image et Applications
EA 3165, Université de La Rochelle
P&ocric;le sciences et Technologies
Avenue Michel Crépeau, 17000
La Rochelle, France
email: nabtia1@gmail.com
|
|---|
Return to the EJDE web page
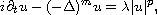
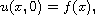
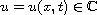 is a complex-valued function,
is a complex-valued function,
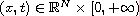 ,
,
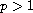 ,
,
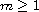 ,
,
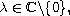 and
and
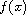 is a given complex-valued function. We prove nonexistence of
a nontrivial global weak solution. Furthermore, we prove that
the
is a given complex-valued function. We prove nonexistence of
a nontrivial global weak solution. Furthermore, we prove that
the
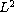 -norm
of the local in time
-norm
of the local in time
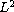 -solution blows
up at a finite time.
-solution blows
up at a finite time.
