We show that the first-order system of difference equations
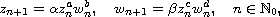
where
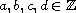 ,
,
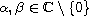 ,
,
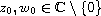 ,
is solvable in closed form,
by finding closed form formulas of its solutions.
,
is solvable in closed form,
by finding closed form formulas of its solutions.
Stevo Stevic
Abstract:
We show that the first-order system of difference equations
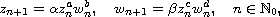
where
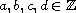 ,
,
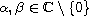 ,
,
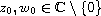 ,
is solvable in closed form,
by finding closed form formulas of its solutions.
,
is solvable in closed form,
by finding closed form formulas of its solutions.
Submitted August 29, 2015. Published December 21, 2015.
Math Subject Classifications: 39A20, 39A45.
Key Words: Difference equation; first order system;product-type system;
solvable in closed form.
Show me the PDF file (283 KB), TEX file, and other files for this article.
 |
Stevo Stevic Mathematical Institute of the Serbian Academy of Sciences Knez Mihailova 36/III, 11000 Beograd, Serbia email: sstevic@ptt.rs |
|---|
Return to the EJDE web page