Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 306, pp. 1-12.
Blow-up for the Euler-Bernoulli viscoelastic equation
with a nonlinear source
Zhifeng Yang, Guobing Fan
Abstract:
In this article, we consider the Euler-Bernoulli viscoelastic equation
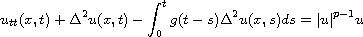
together with some suitable initial data and boundary conditions in
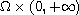 .
Some sufficient conditions on blow-up of
solutions are obtained under different initial energy states.
And from these results we can clearly understand the competitive
relationship between the viscoelastic damping and source.
.
Some sufficient conditions on blow-up of
solutions are obtained under different initial energy states.
And from these results we can clearly understand the competitive
relationship between the viscoelastic damping and source.
Submitted September 1, 2015. Published December 16, 2015.
Math Subject Classifications: 35L35, 35G16.
Key Words: Viscoelastic equation; blow-up; nonlinear source.
Show me the PDF file (252 KB),
TEX file, and other files for this article.
 |
Zhifeng Yang
College of Mathematics and Computer Science
Hunan Normal University
Changsha, Hunan, 410081, China
email: zhifeng_yang@126.com
|
|---|
 |
Guobing Fan
Hunan University of Finance and Economics
Changsha, Hunan 410205, China
email: fan_guobing@126.com
|
|---|
Return to the EJDE web page
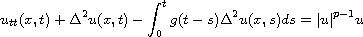
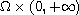 .
Some sufficient conditions on blow-up of
solutions are obtained under different initial energy states.
And from these results we can clearly understand the competitive
relationship between the viscoelastic damping and source.
.
Some sufficient conditions on blow-up of
solutions are obtained under different initial energy states.
And from these results we can clearly understand the competitive
relationship between the viscoelastic damping and source.

