Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 304, pp. 1-8.
Global stability of SIR models with nonlinear incidence
and discontinuous treatment
Mei Yang, Fuqin Sun
Abstract:
In this article, we study an SIR model with nonlinear incidence rate.
By defining the Filippov solution for the model and constructing suitable
Lyapunov functions, we show that the global dynamics are fully determined
by the basic reproduction number
 ,
under certain conditions on the
incidence rate and treatment functions. When
,
under certain conditions on the
incidence rate and treatment functions. When
 the disease-free
equilibrium is globally asymptotically stable, and when
the disease-free
equilibrium is globally asymptotically stable, and when
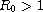 the unique
endemic equilibrium is globally asymptotically stable.
the unique
endemic equilibrium is globally asymptotically stable.
Submitted November 3, 2014. Published December 16, 2015.
Math Subject Classifications: 34A36, 34A60, 34D23.
Key Words: Filippov solution; discontinuous treatment; reproduction number;
asymptotic stability.
Show me the PDF file (201 KB),
TEX file, and other files for this article.
 |
Mei Yang
College of Science
Tianjin University of Technology and Education
Tianjin 300222, China
email: yangmei19890610@yeah.net
|
|---|
 |
Fuqin Sun
College of Science
Tianjin University of Technology and Education
Tianjin 300222, China
email: sfqwell@163.com
|
|---|
Return to the EJDE web page
 ,
under certain conditions on the
incidence rate and treatment functions. When
,
under certain conditions on the
incidence rate and treatment functions. When
 the disease-free
equilibrium is globally asymptotically stable, and when
the disease-free
equilibrium is globally asymptotically stable, and when
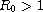 the unique
endemic equilibrium is globally asymptotically stable.
the unique
endemic equilibrium is globally asymptotically stable.

