Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 297, pp. 1-12.
Singular critical elliptic problems with fractional Laplacian
Xueqiao Wang, Jianfu Yang
Abstract:
In this article, we consider the existence of solutions of the critical
problem with a Hardy term for fractional Laplacian
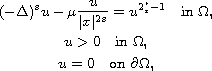
where
 is a smooth bounded domain and
is a smooth bounded domain and
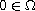 ,
,
 is a positive parameter,
is a positive parameter,
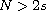 and
and
 ,
,
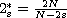 is the critical exponent.
is the critical exponent.
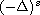 stands for the spectral fractional Laplacian.
Assuming that
stands for the spectral fractional Laplacian.
Assuming that
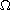 is non-contractible, we show that there exists
is non-contractible, we show that there exists
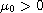 such that
such that
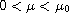 ,
there exists a solution.
We also discuss a similar problem for the restricted fractional Laplacian.
,
there exists a solution.
We also discuss a similar problem for the restricted fractional Laplacian.
Submitted September 6, 2015. Published December 3, 2015.
Math Subject Classifications: 35J20, 35J25, 35J61.
Key Words: Fractional Laplacian; singular critical problem;
non-contractible domain.
Show me the PDF file (252 KB),
TEX file, and other files for this article.
| |
Xueqiao Wang
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: wangxueqiao1989@126.com
|
|---|
 |
Jianfu Yang
Department of Mathematics
Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jfyang_2000@yahoo.com
|
|---|
Return to the EJDE web page
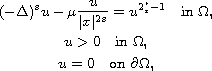
 is a smooth bounded domain and
is a smooth bounded domain and
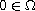 ,
,
 is a positive parameter,
is a positive parameter,
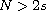 and
and
 ,
,
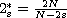 is the critical exponent.
is the critical exponent.
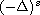 stands for the spectral fractional Laplacian.
Assuming that
stands for the spectral fractional Laplacian.
Assuming that
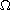 is non-contractible, we show that there exists
is non-contractible, we show that there exists
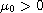 such that
such that
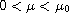 ,
there exists a solution.
We also discuss a similar problem for the restricted fractional Laplacian.
,
there exists a solution.
We also discuss a similar problem for the restricted fractional Laplacian.
