Electron. J. Diff. Equ., Vol. 2015 (2015), No. 290, pp. 1-20.

Asymptotic behavior of the longitudinal permeability of a periodic array of thin cylinders

Paolo Musolino, Vladimir Mityushev

Abstract:
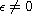We consider a Newtonian fluid flowing at low Reynolds numbers along a spatially periodic array of cylinders of diameter proportional to a small nonzero parameter $\epsilon$. Then for $\epsilon \neq 0$ and close to 0 we denote by $K_{II}[\epsilon]$ the longitudinal permeability. We are interested in studying the asymptotic behavior of $K_{II}[\epsilon]$ as $\epsilon$ tends to 0. We analyze $K_{II}[\epsilon]$ for $\epsilon$ close to 0 by an approach based on functional analysis and potential theory, which is alternative to that of asymptotic analysis. 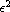We prove that $K_{II}[\epsilon]$ can be written as the sum of a logarithmic term and a power series in $\epsilon^2$. Then, for small $\epsilon$, we provide an asymptotic expansion of the longitudinal permeability in terms of the sum of a logarithmic function of the square of the capacity of the cross section of the cylinders and a term which does not depend of the shape of the unit inclusion (plus a small remainder).

Submitted June 17, 2015. Published November 20, 2015.
Math Subject Classifications: 76D30, 76D05, 35J05, 35J25, 31B10, 45A05.
Key Words: Longitudinal permeability; asymptotic expansion; rectangular array; singularly perturbed domain; integral equations; logarithmic capacity.

Show me the PDF file (315 KB), TEX file, and other files for this article.

Paolo Musolino
Department of Mathematics
University of Padova, Italy
email: musolinopaolo@gmail.com
Vladimir Mityushev
Department of Computer Science and Computational Methods
Pedagogical University of Cracow, Poland
email: mityu@up.krakow.pl

Return to the EJDE web page