Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 289, pp. 1-19.
Singular limiting solutions to 4-dimensional elliptic problems involving
exponentially dominated nonlinearity and nonlinear terms
Sami Baraket, Imen Bazarbacha, Maryem Trabelsi
Abstract:
Let
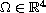 be a bounded open regular set,
be a bounded open regular set,
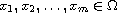 ,
,
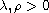 and
and
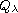 be a non linear operator (which will be defined later).
We prove that the problem
be a non linear operator (which will be defined later).
We prove that the problem
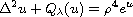
has a positive weak solution in
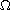 with
with
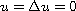 on
on
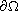 ,
which is singular at each
,
which is singular at each
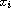 as the parameters
as the parameters
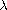 and
and
 tends to 0.
tends to 0.
Submitted August 15, 2015. Published November 20, 2015.
Math Subject Classifications: 35J60, 53C21, 58J05.
Key Words: Biharmonic operator; nonlinear operator; singular limits;
Green's function; nonlinear domain decomposition method.
Show me the PDF file (339 KB),
TEX file, and other files for this article.
 |
Sami Baraket
Department of Mathematics, College of Science
King Saud University, P.O. Box 2455
Riyadh 11451, Saudi Arabia
email: sbaraket@ksu.edu.sa
|
|---|
 |
Imen Bazarbacha
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis
University Tunis El Manar, Tunisia
email: imen.bazarbacha@gmail.com
|
|---|
| |
Maryem Trabelsi
Département de Mathématiques
Faculté des Sciences de Tunis
Campus Universitaire, 2092 Tunis
University Tunis El Manar, Tunisia
email: trabelsi.maryem@gmail.com
|
|---|
Return to the EJDE web page
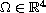 be a bounded open regular set,
be a bounded open regular set,
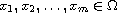 ,
,
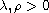 and
and
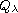 be a non linear operator (which will be defined later).
We prove that the problem
be a non linear operator (which will be defined later).
We prove that the problem
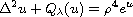
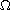 with
with
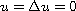 on
on
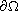 ,
which is singular at each
,
which is singular at each
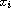 as the parameters
as the parameters
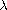 and
and
 tends to 0.
tends to 0.

