Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 288, pp. 1-24.
Holder continuity of bounded weak solutions to generalized parabolic
p-Laplacian equations II: singular case
Sukjung Hwang, Gary M. Lieberman
Abstract:
Here we generalize quasilinear parabolic p-Laplacian type equations to
obtain the prototype equation
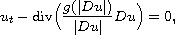
where g is a nonnegative, increasing, and continuous function trapped
in between two power functions
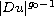 and
and
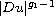 with
with
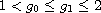 .
Through this generalization in the setting
from Orlicz spaces, we provide a uniform proof with a single geometric
setting that a bounded weak solution is locally Holder continuous
with some degree of commonality between degenerate and singular types.
By using geometric characters, our proof does not rely on any of
alternatives which is based on the size of solutions.
.
Through this generalization in the setting
from Orlicz spaces, we provide a uniform proof with a single geometric
setting that a bounded weak solution is locally Holder continuous
with some degree of commonality between degenerate and singular types.
By using geometric characters, our proof does not rely on any of
alternatives which is based on the size of solutions.
Submitted July 17, 2015. Published November 19, 2015.
Math Subject Classifications: 35B45, 35K67.
Key Words: Quasilinear parabolic equation; singular equation;
generalized structure; a priori estimate; Holder continuity.
Show me the PDF file (343 KB),
TEX file, and other files for this article.
 |
Sukjung Hwang
Center for Mathematical Analysis and Computation
Yonsei University, Seoul 03722, Korea
email: sukjung_hwang@yonsei.ac.kr
|
|---|
 |
Gary M. Lieberman
Department of Mathematics
Iowa State University
Ames, IA 50011, USA
email: lieb@iastate.edu
|
|---|
Return to the EJDE web page
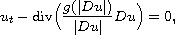
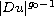 and
and
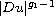 with
with
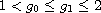 .
Through this generalization in the setting
from Orlicz spaces, we provide a uniform proof with a single geometric
setting that a bounded weak solution is locally Holder continuous
with some degree of commonality between degenerate and singular types.
By using geometric characters, our proof does not rely on any of
alternatives which is based on the size of solutions.
.
Through this generalization in the setting
from Orlicz spaces, we provide a uniform proof with a single geometric
setting that a bounded weak solution is locally Holder continuous
with some degree of commonality between degenerate and singular types.
By using geometric characters, our proof does not rely on any of
alternatives which is based on the size of solutions.

