Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 283, pp. 1-11.
Exponent of convergence of solutions to linear differential equations
in the unit disc
Nacera Berrighi, Saada Hamouda
Abstract:
In this article, we study the exponent of convergence of
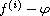 where
where
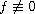 is a solution of linear
differential equations with analytic and meromorphic coefficients in the
unit disc and
is a solution of linear
differential equations with analytic and meromorphic coefficients in the
unit disc and
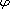 is a small function of
is a small function of
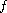 .
From this results
we deduce the fixed points of
.
From this results
we deduce the fixed points of
 by taking
by taking
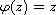 .
We will see the similarities and differences between
the complex plane and the unit disc.
.
We will see the similarities and differences between
the complex plane and the unit disc.
Submitted May 21, 2015. Published November 11, 2015.
Math Subject Classifications: 34M10, 30D35.
Key Words: Linear differential equations; exponent of convergence;
growth of solutions, unit disc.
Show me the PDF file (247 KB),
TEX file, and other files for this article.
 |
Nacera Berrighi
Laboratory of Pure and Applied Mathematics
University of Mostaganem, UMAB, Algeria
email: berrighinacera@univ-mosta.dz
|
|---|
 |
Saada Hamouda
Laboratory of Pure and Applied Mathematics
University of Mostaganem, UMAB, Algeria
email: hamoudasaada@univ-mosta.dz, hamouda_saada@yahoo.fr
|
|---|
Return to the EJDE web page
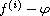 where
where
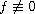 is a solution of linear
differential equations with analytic and meromorphic coefficients in the
unit disc and
is a solution of linear
differential equations with analytic and meromorphic coefficients in the
unit disc and
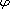 is a small function of
is a small function of
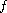 .
From this results
we deduce the fixed points of
.
From this results
we deduce the fixed points of
 by taking
by taking
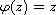 .
We will see the similarities and differences between
the complex plane and the unit disc.
.
We will see the similarities and differences between
the complex plane and the unit disc.

