Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 282, pp. 1-22.
Dynamics of stochastic nonclassical diffusion equations on
unbounded domains
Wenqiang Zhao, Shuzhi Song
Abstract:
This article concerns the dynamics of stochastic nonclassical diffusion
equation on
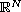 perturbed by a
perturbed by a
 -random
term, where
-random
term, where
![$\epsilon\in(0,1]$](gifs/ac.gif) is the intension of noise.
By using an energy approach, we prove the asymptotic compactness of the
associated random dynamical system, and then the existence of random
attractors in
is the intension of noise.
By using an energy approach, we prove the asymptotic compactness of the
associated random dynamical system, and then the existence of random
attractors in
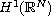 .
Finally, we show the upper semi-continuity
of random attractors at
.
Finally, we show the upper semi-continuity
of random attractors at
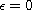 in the sense of Hausdorff semi-metric in
in the sense of Hausdorff semi-metric in
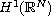 ,
which implies that the obtained family of random
attractors indexed by
,
which implies that the obtained family of random
attractors indexed by
 converge to a deterministic attractor
as
converge to a deterministic attractor
as
 vanishes.
vanishes.
Submitted April 27, 2015. Published November 10, 2015.
Math Subject Classifications: 60H15, 35B40, 35B41.
Key Words: Stochastic nonclassical diffusion equation; random attractor;
asymptotic compactness; weak continuity; upper semi-continuity.
Show me the PDF file (346 KB),
TEX file, and other files for this article.
 |
Wenqiang Zhao
School of Mathematics and Statistics
Chongqing Technology and Business University
Chongqing 400067, China
email: gshzhao@sina.com
|
|---|
 |
Shuzhi Song
School of Mathematics and Statistics
Chongqing Technology and Business University
Chongqing 400067, China
email: 13718903@qq.com
|
|---|
Return to the EJDE web page
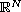 perturbed by a
perturbed by a
 -random
term, where
-random
term, where
![$\epsilon\in(0,1]$](gifs/ac.gif) is the intension of noise.
By using an energy approach, we prove the asymptotic compactness of the
associated random dynamical system, and then the existence of random
attractors in
is the intension of noise.
By using an energy approach, we prove the asymptotic compactness of the
associated random dynamical system, and then the existence of random
attractors in
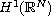 .
Finally, we show the upper semi-continuity
of random attractors at
.
Finally, we show the upper semi-continuity
of random attractors at
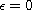 in the sense of Hausdorff semi-metric in
in the sense of Hausdorff semi-metric in
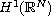 ,
which implies that the obtained family of random
attractors indexed by
,
which implies that the obtained family of random
attractors indexed by
 converge to a deterministic attractor
as
converge to a deterministic attractor
as
 vanishes.
vanishes.

