Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 280, pp. 1-12.
Existence of positive solutions for Kirchhoff problems
Jia-Feng Liao, Peng Zhang, Xing-Ping Wu
Abstract:
We study problems for the Kirchhoff equation
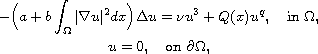
where
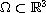 is a bounded domain,
is a bounded domain,
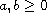 and
and
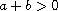 ,
,
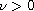 ,
,
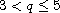 and
and
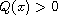 in
in
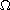 .
By the mountain pass lemma, the existence of positive solutions is
obtained. Particularly, we give a condition of Q to ensure the
existence of solutions for the case of q=5.
.
By the mountain pass lemma, the existence of positive solutions is
obtained. Particularly, we give a condition of Q to ensure the
existence of solutions for the case of q=5.
Submitted June 25, 2015. Published November 10, 2015.
Math Subject Classifications: 35B09, 35B33, 35J20.
Key Words: Kirchhoff type equation; resonance; positive solution;
mountain pass lemma.
Show me the PDF file (254 KB),
TEX file, and other files for this article.
 |
Jia-Feng Liao
School of Mathematics and Statistics
Southwest University
Chongqing 400715, China
email: liaojiafeng@163.com
|
|---|
 |
Peng Zhang
School of Mathematics and Computational Science
Zunyi Normal College
Zunyi, China
email: gzzypd@sina.com
|
|---|
 |
Xing-Ping Wu
School of Mathematics and Statistics
Southwest University
Chongqing 400715, China
email: wuxp@swu.edu.cn
|
|---|
Return to the EJDE web page
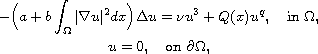
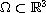 is a bounded domain,
is a bounded domain,
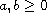 and
and
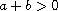 ,
,
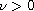 ,
,
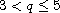 and
and
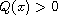 in
in
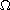 .
By the mountain pass lemma, the existence of positive solutions is
obtained. Particularly, we give a condition of Q to ensure the
existence of solutions for the case of q=5.
.
By the mountain pass lemma, the existence of positive solutions is
obtained. Particularly, we give a condition of Q to ensure the
existence of solutions for the case of q=5.


