Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 279, pp. 1-6.
Solutions to nonlinear Schrodinger equations for special initial data
Takeshi Wada
Abstract:
This article concerns the solvability of the nonlinear Schrodinger
equation with gauge invariant power nonlinear term in one space dimension.
The well-posedness of this equation is known only for
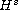 with
with
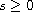 .
Under some assumptions on the nonlinearity, this paper shows that
this equation is uniquely solvable for special but typical initial data,
namely the linear combinations of
.
Under some assumptions on the nonlinearity, this paper shows that
this equation is uniquely solvable for special but typical initial data,
namely the linear combinations of
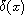 and p.v. (1/x), which belongs to
and p.v. (1/x), which belongs to
 .
The proof in this article allows
.
The proof in this article allows
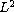 -perturbations
on the initial data.
-perturbations
on the initial data.
Submitted March 27, 2015. Published November 10, 2015.
Math Subject Classifications: 35Q55.
Key Words: Nonlinear Schrodinger Equations; solvability; rough initial data.
Show me the PDF file (194 KB),
TEX file, and other files for this article.
 |
Takeshi Wada
Department of Mathematics
Shimane University
Matsue 690-8504, Japan
email: wada@riko.shimane-u.ac.jp
|
|---|
Return to the EJDE web page
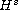 with
with
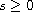 .
Under some assumptions on the nonlinearity, this paper shows that
this equation is uniquely solvable for special but typical initial data,
namely the linear combinations of
.
Under some assumptions on the nonlinearity, this paper shows that
this equation is uniquely solvable for special but typical initial data,
namely the linear combinations of
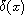 and p.v. (1/x), which belongs to
and p.v. (1/x), which belongs to
 .
The proof in this article allows
.
The proof in this article allows
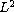 -perturbations
on the initial data.
-perturbations
on the initial data.
