Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 273, pp. 1-13.
Multiple homoclinic solutions for indefinite second-order
discrete Hamilton system with small perturbation
Liang Zhang, Xianhua Tang
Abstract:
In this article, we sutdy the multiplicity of homoclinic solutions to
the perturbed second-order discrete Hamiltonian system
![$$
\Delta[p(n)\Delta u(n-1)]-L(n)u(n)+\nabla W(n,u(n))+\theta\nabla F(n,u(n))=0,
$$](gifs/aa.gif)
where L(n) and W(n,x) are neither autonomous nor periodic in n.
Under the assumption that W(n,x) is only locally superquardic as
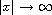 and even in x and F(n,x) is a perturbation term,
we establish some existence criteria to guarantee that the above system has
multiple homoclinic solutions by minimax method in critical point theory.
and even in x and F(n,x) is a perturbation term,
we establish some existence criteria to guarantee that the above system has
multiple homoclinic solutions by minimax method in critical point theory.
Submitted June 9, 2015. Published October 21, 2015.
Math Subject Classifications: 39A11, 58E05, 70H05.
Key Words: Critical point; discrete Hamilton system; homoclinic solution;
small perturbation
Show me the PDF file (262 KB),
TEX file, and other files for this article.
 |
Liang Zhang
School of Mathematical Sciences
University of Jinan
Jinan 250022, China
email: mathspaper2012@163.com
|
|---|
 |
Xianhua Tang
School of Mathematics and Statistics
Central South University
Changsha 410083, China
email: tangxh@csu.edu.cn
|
|---|
Return to the EJDE web page
![$$
\Delta[p(n)\Delta u(n-1)]-L(n)u(n)+\nabla W(n,u(n))+\theta\nabla F(n,u(n))=0,
$$](gifs/aa.gif)
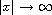 and even in x and F(n,x) is a perturbation term,
we establish some existence criteria to guarantee that the above system has
multiple homoclinic solutions by minimax method in critical point theory.
and even in x and F(n,x) is a perturbation term,
we establish some existence criteria to guarantee that the above system has
multiple homoclinic solutions by minimax method in critical point theory.

