Electron. J. Diff. Equ., Vol. 2015 (2015), No. 267, pp. 1-14.

Stable algorithm for identifying a source in the heat equation

Lahcene Chorfi, Leila Alem

Abstract:
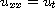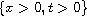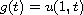We consider an inverse problem for the heat equation $u_{xx}=u_t$ in the quarter plane $\{x>0, t>0\}$ where one wants to determine the temperature $f(t)=u(0,t)$ from the measured data $g(t)=u(1,t)$. This problem is severely ill-posed and has been studied before. It is well known that the central difference approximation in time has a regularization effect, but the backward difference scheme is not well studied in theory and in practice. In this paper, we revisit this method to provide a stable algorithm. 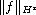Assuming an a priori bound on $\|f\|_{H^s}$ we derive a Holder type stability result. We give some numerical examples to show the efficiency of the proposed method. Finally, we compare our method to one based on the central or forward differences.

Submitted June 27, 2015. Published October 16, 2015.
Math Subject Classifications: 35K05, 65M32, 65T50.
Key Words: Inverse problem; heat equation; fourier regularization; finite difference.

Show me the PDF file (307 KB), TEX file, and other files for this article.

Lahcène Chorfi
Laboratoire de Mathématiques Appliquées
Université B. M. d'Annaba
B.P. 12, 23000 Annaba, Algérie
email: l_chorfi@hotmail.com
Leïla Alem
Laboratoire de Mathématiques Appliquées
Université B. M. d'Annaba
B.P. 12, 23000 Annaba, Algérie
email: alemleila@yahoo.fr

Return to the EJDE web page