Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 266, pp. 1-15.
Infinitely many sign-changing solutions for concave-convex
elliptic problem with nonlinear boundary condition
Li Wang, Peihao Zhao
Abstract:
In this article, we study the existence of sign-changing
solutions to
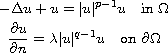
with
 and
and
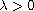 .
By using a combination of invariant sets and Ljusternik-Schnirelman
type minimax method, we obtain two sequences of sign-changing solutions
when p is subcritical and one sequence of sign-changing solutions
when p is critical.
.
By using a combination of invariant sets and Ljusternik-Schnirelman
type minimax method, we obtain two sequences of sign-changing solutions
when p is subcritical and one sequence of sign-changing solutions
when p is critical.
Submitted August 30, 2015. Published October 16, 2015.
Math Subject Classifications: 35J60, 47J30, 58E05.
Key Words: Nonlinear boundary condition; concave-convex; invariant sets;
sign-changing solutions.
Show me the PDF file (242 KB),
TEX file, and other files for this article.
 |
Li Wang
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: lwang10@lzu.edu.cn
|
|---|
 |
Peihao Zhao
School of Mathematics and Statistics
Lanzhou University
Lanzhou 730000, China
email: zhaoph@lzu.edu.cn
|
|---|
Return to the EJDE web page
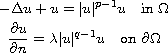
 and
and
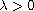 .
By using a combination of invariant sets and Ljusternik-Schnirelman
type minimax method, we obtain two sequences of sign-changing solutions
when p is subcritical and one sequence of sign-changing solutions
when p is critical.
.
By using a combination of invariant sets and Ljusternik-Schnirelman
type minimax method, we obtain two sequences of sign-changing solutions
when p is subcritical and one sequence of sign-changing solutions
when p is critical.

