In this article, we study the Kirchhoff equation
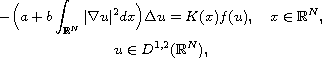
where
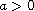 ,
,
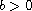 and
and
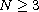 .
Under suitable conditions on K and f,
we obtain four existence results and two nonexistence results, using
variational methods.
.
Under suitable conditions on K and f,
we obtain four existence results and two nonexistence results, using
variational methods.
Yu Duan, Jiu Liu, Chun-Lei Tang
Abstract:
In this article, we study the Kirchhoff equation
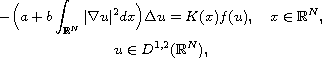
where
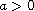 ,
,
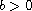 and
and
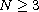 .
Under suitable conditions on K and f,
we obtain four existence results and two nonexistence results, using
variational methods.
.
Under suitable conditions on K and f,
we obtain four existence results and two nonexistence results, using
variational methods.
Submitted September 7, 2015. Published October 8, 2015.
Math Subject Classifications: 35J20, 35J60, 35A01.
Key Words: Kirchhoff equation; subcritical growth; zero mass;
Pohozaev identity.
Show me the PDF file (272 KB), TEX file, and other files for this article.
 |
Yu Duan School of Mathematics and Statistics Southwest University Chongqing 400715, China email: duanyu3612@163.com |
|---|---|
 |
Jiu Liu School of Mathematics and Statistics Southwest University Chongqing 400715, China email: jiuliu2011@163.com |
 |
Chun-Lei Tang School of Mathematics and Statistics Southwest University Chongqing 400715, China Phone +86 23 68253135, Fax +86 23 68253135 email: tangcl@swu.edu.cn |
Return to the EJDE web page