Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 251, pp. 1-12.
Lattice Boltzmann method for coupled Burgers equations
Yali Duan, Linghua Kong, Xianjin Chen
Abstract:
In this paper, we propose a lattice Boltzmann model for coupled
Burgers equations (CBEs). With a proper time-space scale and the
Chapman-Enskog expansion, the governing equations are recovered
successfully from the lattice Boltzmann equations, and the resulting
local equilibrium distribution functions are also obtained.
The partial derivative
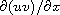 in the model
is treated as a source term and discretized with a 2nd-order central
difference scheme. Numerical experiments show that the numerical results
by the Lattice Boltzmann Method (LBM) either agree well with the
corresponding exact solutions or are quite comparable with those available
numerical results in the literature.
in the model
is treated as a source term and discretized with a 2nd-order central
difference scheme. Numerical experiments show that the numerical results
by the Lattice Boltzmann Method (LBM) either agree well with the
corresponding exact solutions or are quite comparable with those available
numerical results in the literature.
Submitted May 1, 2015. Published September 25, 2015.
Math Subject Classifications: 65M12, 65M99.
Key Words: Lattice Boltzmann model; equilibrium distribution;
coupled Burgers equations; Chapman-Enskog expansion.
Show me the PDF file (466 KB),
TEX file, and other files for this article.
 |
Yali Duan
School of Mathematical Sciences
University of Science and Technology of China
Hefei, Anhui 230026, China
email: ylduan01@ustc.edu.cn
|
|---|
 |
Linghua Kong
School of Mathematics and Information Science
Jiangxi Normal University
Nanchang, Jiangxi, 330022, China
email: konglh@mail.ustc.edu.cn
|
|---|
 |
Xianjin Chen
School of Mathematical Sciences
University of Science and Technology of China
Hefei, Anhui 230026, China
email: chenxjin@ustc.edu.cn
|
|---|
Return to the EJDE web page
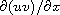 in the model
is treated as a source term and discretized with a 2nd-order central
difference scheme. Numerical experiments show that the numerical results
by the Lattice Boltzmann Method (LBM) either agree well with the
corresponding exact solutions or are quite comparable with those available
numerical results in the literature.
in the model
is treated as a source term and discretized with a 2nd-order central
difference scheme. Numerical experiments show that the numerical results
by the Lattice Boltzmann Method (LBM) either agree well with the
corresponding exact solutions or are quite comparable with those available
numerical results in the literature.


