Electron. J. Diff. Equ.,
Vol. 2015 (2015), No. 250, pp. 1-9.
Regularity for the axisymmetric Navier-Stokes equations
Peng Wang
Abstract:
In this article, we establish a regularity criterion for the Navier-Stokes
system with axisymmetric initial data. It is proved that if the
local axisymmetric smooth solution
 satisfies
satisfies
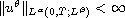 ,
where
,
where
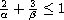 ,
and
,
and
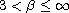 ,
then the strong solution keeps smoothness up
to time T.
,
then the strong solution keeps smoothness up
to time T.
Submitted June 11, 2015. Published September 25, 2015.
Math Subject Classifications: 35Q30, 76D03.
Key Words: Navier-Stokes equations; axi-symmetric flow;
regularity criterion.
Show me the PDF file (222 KB),
TEX file, and other files for this article.
 |
Peng Wang
Department of Mathematics
Zhejiang Normal University
Jinhua 321004, Zhejiang, China
email: wpmath2013@gmail.com
|
|---|
Return to the EJDE web page
 satisfies
satisfies
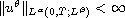 ,
where
,
where
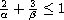 ,
and
,
and
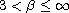 ,
then the strong solution keeps smoothness up
to time T.
,
then the strong solution keeps smoothness up
to time T.
