Electron. J. Diff. Equ., Vol. 2015 (2015), No. 246, pp. 1-11.

Limit cycles bifurcating from the period annulus of a uniform isochronous center in a quartic polynomial differential system

Jackson Itikawa, Jaume Llibre

Abstract:
We study the number of limit cycles that bifurcate from the periodic solutions surrounding a uniform isochronous center located at the origin of the quartic polynomial differential system
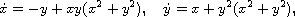
$$ \dot{x}=-y+xy(x^2+y^2),\quad \dot{y}=x+y^2(x^2+y^2), $$
when perturbed in the class of all quartic polynomial differential systems. Using the averaging theory of first order we show that at least 8 limit cycles bifurcate from the period annulus of the center. Recently this problem was studied by Peng and Feng [9], where the authors found 3 limit cycles.

Submitted October 15, 2014. Published September 22, 2015.
Math Subject Classifications: 34A36, 34C07, 34C25, 37G15.
Key Words: Polynomial vector field; limit cycle; averaging method; periodic orbit; uniform isochronous center.

Show me the PDF file (217 KB), TEX file, and other files for this article.

  Jackson Itikawa
Departament de Matemàtiques
Universitat Autònoma de Barcelona
08193 Bellaterra, Barcelona, Catalonia, Spain
Fax +34 935812790. Phone +34 93 5811303
email: itikawa@mat.uab.cat
Jaume Llibre
Departament de Matemàtiques
Universitat Autònoma de Barcelona
08193 Bellaterra, Barcelona, Catalonia, Spain
Fax +34 935812790. Phone +34 93 5811303
email: jllibre@mat.uab.cat

Return to the EJDE web page